Inverted Phase

Many tweaks in my audiophile journey are discovered by accident. In this blog we will talk about one of the best kept hifi secrets - phase.
A surprisingly large number of people wired their system up wrongly, getting the left and right channels mixed up is more common than you think! But phase is something more difficult, and tend to catch people off guard.
Phase (also known as polarity for audio) is a common issue for people with balanced gear, however it may apply to single ended equipment as well in very rare cases.
In the past I was unaware of any reliable ways to test for this, until the Don pointed out the pop test.
More on this later, let's get some of the basics out of the way first.
Let's demystify what phase is. We begin first by discussing time.
Time is usually used as a counter, to count the length of time to perform a particular task, e.g. 3 hours to roast a pork belly, or 10 hours from point A to point B. However we can also use time to track the life cycle of an event, e.g. the change from day to night, the changing seasons, high/low tides and so on.
In the first instance we are using time like a ruler, measuring a quantity known as time (function of time) like placing a piece of a string against a ruler to find it's length. In the second case we are using time to describe the property of periodicity (function of frequency). In this second example, think of time the hands of a clock rotating around in circles. The number of rotations don't really matter per se. For a clock, what is important is where the minute and hour hands are on the clock face.
Relationship of Time And Angles
Below is a picture of a sine wave. Time is the X axis (horizontal bar with the label Time, t). There is a simple reason why we use degrees as our unit of measurement is simple. Waves have a unique physical property - at a certain point in time, the wave will revert to it's original state and repeat itself. In other words, when the wave reaches 360°, the counter is reset to 0° and the whole process starts again. Like a clock striking midnight: a new day beckons, a new cycle begins.
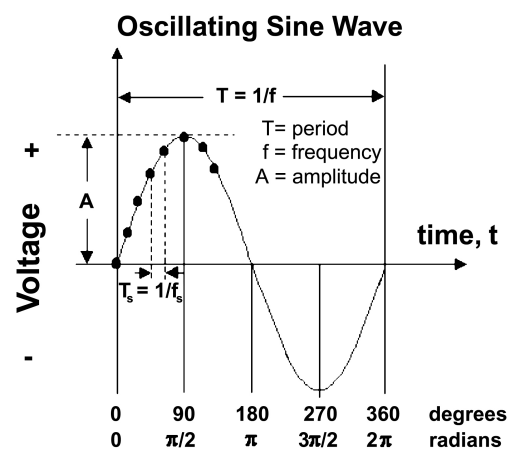
The graph above (Credit: Wikipedia) is like unwrapping the circle of a clock into a straight line. If you extend the wave beyond 360°, the amplitude of t = 15° will be equivalent to t = 375°, 360° = 720°, and so on. This wrapping phenomenon is the reason why we use degrees. A picture speaks a thousand words, an animated GIF even more.
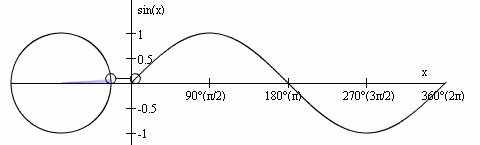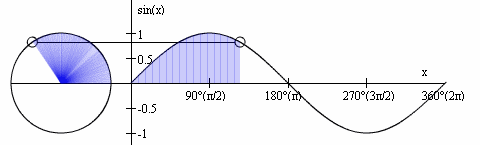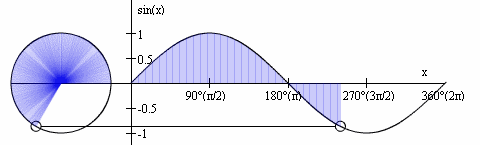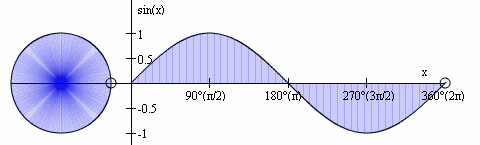
We only need to concern ourselves with waves when t=0°, and t=360° due to this cyclical property. The time taken to complete a cycle is called the period (T) of the wave (with the units of seconds). To get the angle, we divide this T into 360°. Anything beyond T are simply multiples of T - 0° to 720° is 2T, 0° to 1080° is 4T and so on. By focusing just on T, we are effectively breaking a big problem down into a smaller and simpler problem that's easier to solve.
In audio, it is preferable to use the unit frequency (Hz) instead of period, frequency is really 1/T and is the preferred units because we are dealing with shorter periods in audio. The two units are interchangeable and which unit to use depends on the physical application. e.g. In oceanography, waves have longer periods and thus people prefer to use periods instead (i.e. this is a 20 second period rather than 0.05 Hz wave).
A cycle is where a wave cross the Y=0 mark as shown above. One important note is this Y=0 is the zero crossing and not necessarily a numerical 0. In the physical world, this zero crossing is usually the median value. All measured values are normalised to this median. What this means is all physical measured values have the median subtracted. Any value greater than the median becomes positive, any below becomes negative, and the median is the new zero.
So what is phase then?
In the context of this article, it's the starting angle (along the X-axis, time) where the wave begins relative to a reference. And in the case of audio, the reference is anywhere when Y = 0 (0 voltage).
Think of phase as asking the question of 'does it line up'? If your system is wired correctly, the phase will be 0° (this means in phase), and the phase is 180° if wired incorrectly (referred to as out of phase).
What is Inverted Phase
An inverted phase is where the wave form is the opposite to the original waveform (In our example the magnitude is shifted 180° from the normal wave). In layman terms, if you are in phase, positive (+) remains as positive (+) but when you have inverted phase, positive (+) becomes negative (-).
Note that a wave with inverted phase cannot exist on it's own. Inversion is a property and describes a relationship relative to another wave form. On it's own the wave form from the previous page and the one below are separate entities. But when compared together one is the inverse of the other, like mirror reflections of each other.
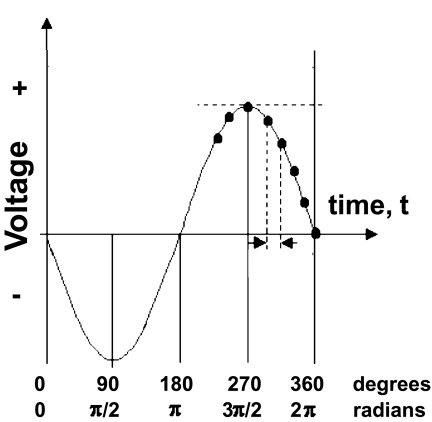
Another way of looking at this is every value on the Y axis has a factor of -1 applied to it. Keep multiplying by -1 again and again and you switch from normal and it's inverse. Inversion is switching the sign from positive to negative and vice versa. Sign is also known as polarity, as such inverted polarity is another term we use to describe this.
Incidentally there is a very special property when you sum the wave and it's inverse together - the magnitude will be 0 at every angle. The two waves effectively cancel each other out. If you have a mono signal feeding to two speakers, if you wire only one speaker out of phase and line them up you might hear nothing (or close to nothing). How cool is that?
In typical stereo setups though the only issue we are interested in are the relative phase at 0° and 180°. The goal is to have a system that wired up for in phase. Positive has to mean positive (+).
How Do You Get Inverted Phase
Here are the common mistakes that I'm aware of as the cause of phase inversion:
- Incorrect wiring: How often did you make this mistake of connecting the amplifier positive to the speaker negative and vice versa? It's easier to make this error than you think!
- Mixing balanced Europe gear with balanced US gear: XLR gears have 3 pins - positive (+), negative (-) and ground. In Europe the convention is to use XLR system where pin 2 is positive (2 hot) while United States system denote pin 3 as positive (3 hot). Mixing components from both side of the pond will connect the positive (+) from one system to the negative (-) of another. Sure fire way to end up with a system on the inverted phase.
- Inverted phase Single Ended gear: Singled ended gear basically means unbalanced system (RCA is the usual connector used). In some rare instances I think the negative phase is used as positive.
The above is not the end of the story, as you can compound the issues by mixing balanced US and Europe together, wire your speakers wrongly and then add an unbalanced pre amplifier with a negative phase.
You may be using a balanced CD player and an unbalanced DAC as your two sources, but you connect them to a balanced pre from US and a balanced power amplifier from the EU.

The combinations is endless, it gets real confusing real quickly!
Is This Audible?
Many people would be rolling on the floor laughing in stitches right now. "This post is too funny! It's not audible! This is snake oil!", they'd say. Is this for real?
One speaker out of phase is definitely an issue as the bass canceled out, but who cares anyway as long as both speakers are in the same phase? To be honest I do not have the answer. Put it this way, if this is not an issue, this blog post will not exist.
For me personally when phasing becomes an issue, they are very obvious.
- The sound stage collapse and the image width and height is not as wide or high as before. Everything is in the middle, there are no sounds coming from the extreme left or extreme right. At this you feel like you are in a headfi setup.
- There are 'holes' in the sound stage. A very common phenomenon would be a distinct left speaker, distinct right speaker, and a narrow phantom center. And nothing else any where.
- Vocals tend to "hang low" to the floor, sometimes even as low as ground level
These are the only some of the objective issues I am aware of. But it is deeper than that, the one issue I have with an incorrect phase that stood out to me is subjectively the whole music not only sound wrong, it feels wrong and there is absolutely no emotional connection at all to the music.
Over the years I have tried to play and replay both versions to different people, using different gear at different levels and so on.Unfortunately the verdict is still open, all agreed there are differences, but it's not conclusive which is better. And we have no way of knowing which phase is actually the correct one either as none of us produced these source materials.
Perhaps with a bit of analysis it may be possible to determine the phase. Something worth investigation in the future I guess.
How To Diagnose Phase
Did I ever mention I nearly wanted to pull my hair out. Is there a solution? Thanks to the Don, yes there is an easy way to determine your system's phase (i.e. test if positive is positive). And it is a very simple test.
All you need to do is play a known input signal called "Speaker Pop".
The following picture shows the wave form of a speaker pop track (Courtesy Studio Six). The entire waveform is above the zero crossing. There are no values below the zero crossing at all. When you are playing this track in your audio setup, there is only voltage on the positive (+) wire and nothing on the negative (-) wire.
Sharp minded readers will recognise this waveform as a simple digital pulsating direct current (DC). DC basically means always positive while AC (alternating current) switches polarity over time.
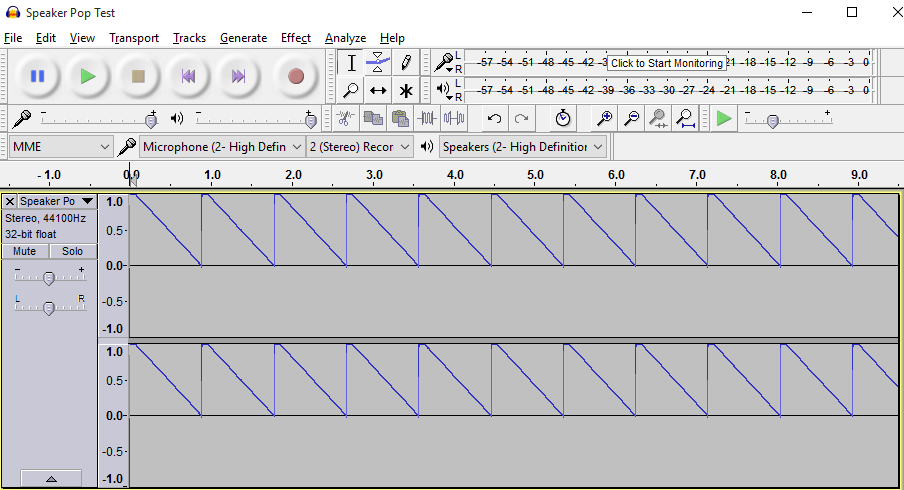
When you are playing this track, your drivers only move forward from rest (0), and from forward back to rest again. In layman terms this means you'd literally see the driver 'popping out'. Confirm your drivers are doing this, this means your speakers are in phase.
If your system is phase inverted, your drivers will be 'sucking in' instead of 'pushing out' when playing this track. If you see this, your setup is out of phase.
So do you get the joke now from the first page? Notice how everything seem to be drawn into the speaker rather than blown away like the classic picture? It's a reference the drivers are sucking in more than it's pushing out.

In general phase issues that are audible tend to be caused by mid-range and sub-woofers. Just confirming these two should be enough. For testing tweeters' phase you'd require an iPhone. Also, I think it's possible for tweeters to be wired 180° out of phase with the woofers. So do not be worried if your tweeters are not in phase as it's the biggest drivers we are focusing here.
Demonstration
If you're still confused at everything I just said, here is a video showing this effect (around 2:10 mark). Notice how when given a positive DC, the cone moves out. All you need to do is to setup your system as so.
Personally I wouldn't recommend a DC battery for obvious reasons - it wouldn't work as we are testing the phase of the entire system, not just the speaker cabling.
And the even more obvious reason, feeding a constant DC to the coil will damage the speakers. Do not even attempt to do this if you have no idea what you're doing. Notice how quickly he did the test? Do not even try this at home.
The speaker pop test is the only safe way to go (thanks again Don!). Also, I do not recommend running this speaker pop test for long periods, who knows if you'd melt or burn out the speaker if you do this continuously?
Personally I do not run this test for longer than 10 seconds, and I tend to wait around 60 seconds between each 10 second est.
Do not hold me liable for any damages. Do this at your own risk. So far the best tool I know of is Speaker Polarity from Studio Six. Unfortunately this requires a iPhone and is a paid app so Android fans (like me) are out luck.
For better or worse, there are DACs out there with safety features built in that detects the presence of DC and cut its output. Unfortunately if you are using DACs like these you'd need to find another way to find the phase of your audio setup (ears are a good tool).
Sure you can always use another DAC to get this test track playing, but you'd never know the phase of your DAC.
What about those "in-phase, out-of-phase" test tracks from audiophile CDs? Maybe they'd work for you but they all sound the same to me. From what I can hear, they are telling you if both speakers are in phase, or one of the speaker is out of phase, but it's relative to the speaker. The speaker pop test, will tell you the phase relative to the signal - feed a positive pulsed DC, you get a speaker cone that can only move forward.
Easy as!
Final Notes
As mentioned before, some music are recorded in the wrong phase so knowing the phase of your system allows you make the correct assessment (and adjustments) when playing these tracks. The music you are playing may well be recorded, or mixed with incorrectly setup systems.
So while your system is setup correctly at 0°, the music is recorded, mixed at 180°. When playing these music,you are still playing them with the wrong phase. If some tracks don't sound good to you, invert the phase and see how that goes.
As always, listen to music by listening to the music. Do not over analyse. Simply sit back, relax and let the music (and the emotions) take you for a ride. Over analyse, and you become this guy below - completely missing the point of a hi fi setup.

So there you have it. Phase demystified I hope. Setup your system to be in phase, using the method you're most comfortable with. If you are interested to use your ears to test for inverted phase, refer to this forum thread for a list of tracks that may1 be out of phase (link).
1 May because the verdict is still open if these tracks are truly out of phase, or not.



Add new comment